Recently there’s a breakthrough in the quantum computational complexity research, which implies a fruitful of interesting results. As a beginer of quantum information, I thought it is worthy of “excerpting” some important ideas provdied in the original 160+ page paper.

The following sections will be in accord with the original paper’s chapters, which includes both the background and some technical results.

It’s always fun to organize knowledge and distill it to a simpler form. I’m happy to get a chance to share my understanding of quantum computation with a group of talented engineers, and I hope to deliver concepts with as much intuitive examples as possible.

In this post, I share two of my quantum computation slides. The first one is quantum computation 101, which established foundation and intuitions of quantum computation. The second goes on to explore topics of machine learning and its’ interplay with quantum computation.

Btw, some of the ‘puns’ or acronym used in the slides are purely mandarine, only to catch the attention of my chinese-speaking audiences.

Given a divergence measure $d(P, Q)$ and two distribution $P$ $Q$, what is the effect to the divergence $d(P^m, Q^m)$ as $m$ increases ? Intuitively, the divergence shall increase since product distribution emphasize the difference of the distribution. In this work by Zinan et.al , the upper and lower bound of $d(P^m, Q^m)$ is given for the divergence measure :

\begin{eqnarray} && d _{p}(P,Q) = \mathop{\sup} _{S} [P(S) - Q(S)] \end{eqnarray}

This measure is closely related to the optimal successful detection probability $P _{\rm opt}$ in the binary hypothesis testing :

\begin{eqnarray} && P _{\rm opt} = \mathop{\sup} _{S} [\pi _1 P(S) + \pi _2 (1 - Q(S))] = \pi _2 + d _{p}(\pi _1 P, \pi _2 Q) = \frac{1}{2} + d _{\rm TV}(\pi _1 P, \pi _2 Q)
\end{eqnarray}

where $\pi _1, \pi _2$ are the prior distribution of the hypothesis, and $d _{\rm TV}(P, Q)$ is the total variance distance :

\begin{eqnarray} && d _{TV}(P,Q) = \frac{1}{2} \sum _{\omega \in \Omega} |P(\omega) - Q(\omega)| \end{eqnarray}

What makes the work by Zinan et.al interesting is that if certain local property is satisfied for the distribution pair $(P, Q _1)$ but not for $(P, Q _2)$, and assume $d _p(P, Q _1) = d _p(P, Q _2)$, then the possible value region of $d _p(P^m, Q^m _1)$ splits away from that of $d _p(P^m, Q^m _2)$. This local property is called $(\epsilon, \delta)$ -mode collapse, defined as:

\begin{eqnarray} && P,Q \; {\rm has \; (\epsilon, \delta)- mode \; collapse \; :}\exists S \; {\rm s.t.} \; P(S) \geq \delta \; , Q(S) \leq \epsilon \end{eqnarray}

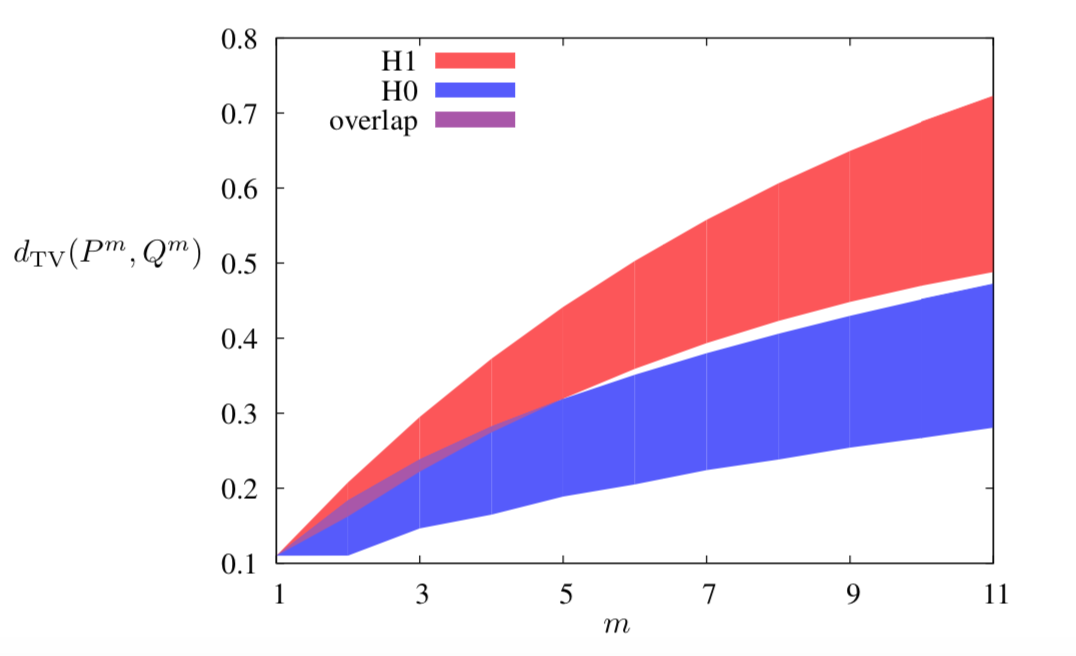
Interestingly, similar result was given in the quantum literature by Jonas Maziero for trace distance:

\begin{eqnarray} && d _1 (\rho _1, \rho _2) = \frac{1}{2} \Vert \rho _1 - \rho _2 \Vert _1 = {\rm Tr} (\sqrt{(\rho _1 - \rho _2)^{\ast} ( \rho _1 - \rho _2)}) \end{eqnarray}

So, I think it would be fun to dig into the quantum counterpart of Zinan’s work.

Recently a bunch of Generative Adversarial Net (GAN) related research has boomed in the unsupervised learning community, and it seems interesting to fully understand the mechanism of this novel learning framework. Just a few days ago (July 5th, 2018), Alexia Jolicoeur-Martineau et al proposed a Relativistic GAN that aimed to provide improvement via changes of the discriminator term in the original GAN objective function. It pointed out that the real data are usually ignored during the learning process in most GAN paradigm, and thus it proposed a relativistic quantity to measure how ‘real’ the real samples are compared to the fake sample.

The following notes are summarized from Prof I-Hsiang Wang’s lecture: Mathematic Principles of Machine learning, Lec 3. An alternated derivation is also given in the website note and summarized here.

The following notes are summarized from Prof I-Hsiang Wang’s lecture: Mathematic Principles of Machine learning, covering lecture 1 and 2.

Given $n$ independently distributed sub-gaussian random variable $Z_i$, each has bounded MGF due to sub gaussian property:

\begin{eqnarray} && E[e^{Z_i}] \leq e^{\lambda^2 \sigma^2 /2 } \;\;\; \forall i = 1 \dots n \end{eqnarray}

for some $\lambda$ being postive real number. Let $X = \mathop{\max}_{1\leq i \leq n } Z_i$, one has that:

\begin{eqnarray} && E[X] \leq \sigma \sqrt{2 \log n} \end{eqnarray}

In this post, a quantum adiabatic method applied to search problem is summarized and commented. All the following context is based on $\rm Quantum \, Search \, by \, Local \, Adiabatic \, Evolution$ from J$\acute{e}$r$\acute{e}$mie Roland and Nicolas J. Cerf.